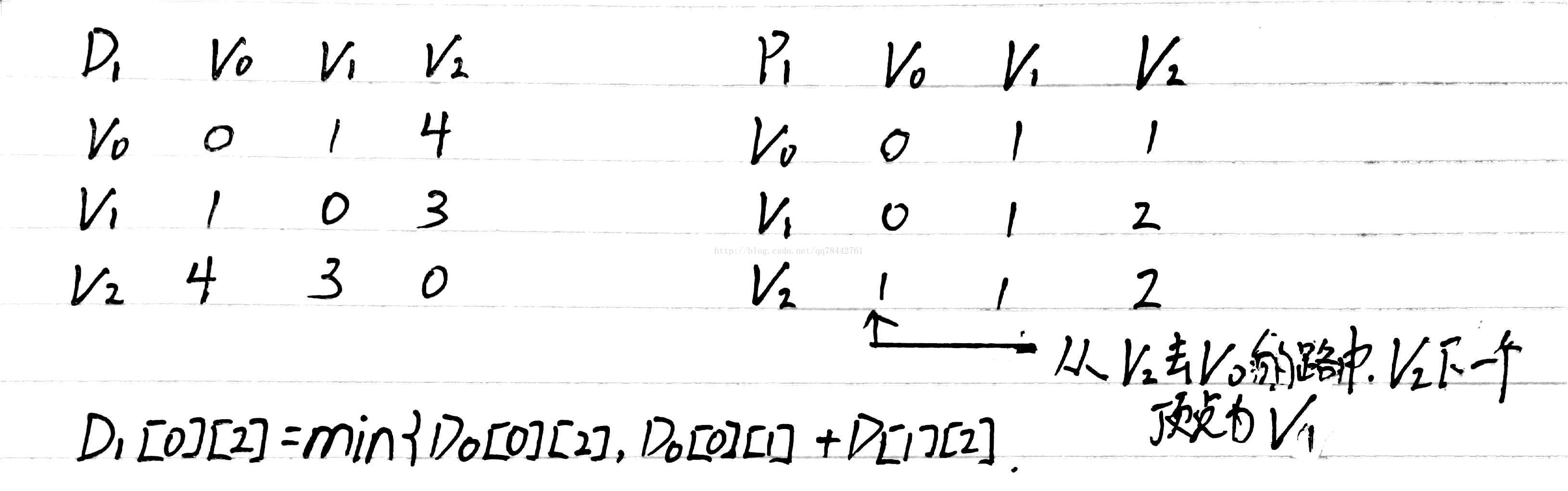最短路径(弗洛伊德算法)-ag真人游戏

迪杰特斯拉算法求的是一个顶点到所有顶点的最短路径，但弗洛伊德算法是求所有顶点到所有顶点的最短路径。

首先，来看下面这个简单的图：

我们把他的邻接矩阵和初始化的p做出来，如下图所示：

代码如下：

#define maxvex	9
#define infinity	65535
typedef int pathmatirx[maxvex][maxvex];
typedef int shortpathtable[maxvex][maxvex];
void shortestpath_floyd(mgraph g, pathmatirx *p, shortpathtable *d)
{
	int v, w, k;
	
	// 初始化d和p
	for( v=0; v < g.numvertexes; v   )
	{
		for( w=0; w < g.numvertexes; w   )
		{
			(*d)[v][w] = g.matirx[v][w];
			(*p)[v][w] = w;
		}
	}
	
	// 优美的弗洛伊德算法
	for( k=0; k < g.numvertexes; k   )
	{
		for( v=0; v < g.numvertexes; v   )
		{
			for( w=0; w < g.numvertexes; w   )
			{
				if( (*d)[v][w] > (*d)[v][k]   (*d)[k][w] )//下标为k顶点路径比原两点间更短，设置更小的那个
				{
					(*d)[v][w] = (*d)[v][k]   (*d)[k][w];
					(*p)[v][w] = (*p)[v][k];		//路径设置经过下标为k的顶点
				}
			}
		}
	}
}

由(*d)[v][w]>(*d)[v][k] (*d)[k][w]

指的是下面这个，并且d1和p1化为